Tu utilises les fonctions tous les jours !
Ahhhh... les fonctions, ces objets mathématiques qui sont et resteront très obscurs pour beaucoup de lycéens. Peut-être que c'est ton cas ? Penses-tu avoir bien compris ce qu'est une fonction ? Saisis-tu toutes les formes qu'une fonction peut prendre ? En es-tu sûr ?
J'ai écrit cet article pour te donner une vision simple de ce qu'est une fonction et des 10 points essentiels qu'il faut connaitre absolument ! Prends le temps de le lire, les fonctions sont partout et si tu vises le BAC, tu n'auras pas d'autres choix que de bien les comprendre. D'ailleurs même si tu n'as peut-être pas encore fait le lien avec les maths, tu utilises des fonctions en permanence... je m'explique tout de suite.
Mettre en relation grâce aux fonctions.
Explication du titre obscur ci-dessus.
Dans la nature, et plus généralement dans la vie, énormément de choses sont reliées entre elles. Par exemple, le poids d’une pomme est reliée à l’âge qu’elle a, la luminosité du ciel est essentiellement reliée à l’heure qu’il est, la distance qu’un animal parcourt en un certain temps est directement reliée à la vitesse à laquelle il court, …
En fait, une fonction c'est simplement la façon matheuse d'écrire une relation entre deux objets. D'où le titre obscur : on peut mettre en relation (deux objets) grâce aux fonctions. Ça parait moins obscur dit comme ça, non ? Peut-être que j'aurais dû te dire ce que j'appelle un objet ? Eh bien, je dirais que ça peut être n'importe quoi tant que ça peut se mesurer d'une façon ou d'une autre. Car, comme souvent quand on veut faire des maths, il faut travailler avec des choses que l'on peut mesurer. Euh, toujours pas clair ? Je te donne un exemple tout de suite pour visualiser tout ça.
Un exemple simple... mais ennuyeux.
Illustrons ça tout de suite avec un exemple hyper simple... mais très chiant. Quand t'achètes des fruits (wouhou), il existe une relation entre le prix (le premier objet) et le poids (le deuxième objet) de ces fruits. Autrement dit, une relation entre 2 objets qui se mesurent, le prix qui se mesure en € et le poids qui se mesure en kilo par exemple.
Bien que très bateau comme exemple, il est pas mal car la relation entre ces 2 objets est une des plus simples qui existe. En effet, il suffit de multiplier le poids par le prix au kilo pour obtenir le prix. Autrement dit, prix = (prix/kilo) * poids ! Normalement, ça devrait te rappeler la première fonction que tu as vue dans ta vie, la fonction linéaire : f(x) = a*x. Dans ce cas précis, f(x) te donne le prix des fruits avec a qui est le le prix/kilo et x le poids des fruits. Passons à des fonctions plus intéressantes, tu veux bien ?
Le monde se décrit avec des fonctions...
Il y a une science dans laquelle on utilise plein de fonctions pour décrire comment le monde fonctionne (fonction, fonctionne... tu vois le lien est même dans la langue française !), c'est la Physique. Très souvent d'ailleurs tu utilises de nouvelles notions de maths en physique (pour moi, c'était la fonction exponentielle) avant de les voir en maths... oui c'est bien fait n'est-ce pas ?
Depuis toujours les scientifiques qui essaient de décrire le monde utilisent des fonctions. De la force exercée par un ressort
en fonction de ses caractéristiques à la propagation de la chaleur dans une salle en fonction d'une source de chaleur (radiateur par exemple) en passant par les trajectoires des planètes, tout est représenté par des fonctions. Autant te dire qu'une fonction peut vite devenir très complexe avec une formule absolument illisible. Si tu as jeté un œil aux liens des exemples, tu vois de quoi je parle. Mais ce qu'il faut bien comprendre, c'est que même avec une formule horrible,
une fonction reste la façon matheuse de dire qu'un truc dépend d'un autre et de décrire comment !
Ce que tu dois bien comprendre !
Par conséquent, ton boulot quand tu es face à une fonction c’est de comprendre :
- Ce que la fonction permet de calculer ? C'est ce que je vais appeler la sortie. (le prix des fruits)
- Ce qu'elle a besoin pour calculer cette sortie ? Je vais appeler ça l'entrée. (le poids des fruits)
- Et comment elle relie les deux ? C'est ce que donne la formule. (entrée multipliée par prix/kilo)
Une fonction en Maths est donc la formule qui permet de calculer la sortie en fonction de l'entrée. Dans la suite de cet article, je vais beaucoup utiliser les mots entrée, sortie et formule, donc si tu n'as pas bien compris, relis l'explication jusqu'à ce que ce soit clair. Je t'ai mis une petite illustration, ça te parlera peut-être mieux ?

Si tu as ça en tête, le reste de ce qu’on va te demander sur les fonctions n’est « que » des maths qui n’ont rien de spécifique et que tu sais déjà faire dans 90 % des cas !
Dans la partie suivante, j'ai pris le temps de te lister le plus clairement possible les 10 points à absolument connaître sur les fonctions. Note bien qu'ils sont toujours vrais pour toutes les fonctions ! Pour cette raison, si tu prends le temps de bien saisir ces 10 points, tu pourras dire que tu as compris ce que sont les fonctions et tu seras capable de les utiliser en maths pour faire monter ta moyenne !
10 points essentiels sur les fonctions.
Avant de te lister les 10 points que tu dois toujours avoir en tête quand tu travailles avec les fonctions, je voudrais parler rapidement des notations. Je ne t'apprends rien, on utilise très souvent x pour l'entrée, y pour la sortie et f pour nommer la fonction, ce qui donne comme formule y = f(x). Ces lettres n'ont aucune importance, ce qui veut dire que tu ne dois jamais considérer que x est toujours l'entrée ou y toujours la sortie !
Les lettres sont juste un truc pour pouvoir écrire en maths tout ce dont j’ai parlé avec des mots avant, sinon ça donnerait : sortie = fonction(entrée), ce qui serait un peu chiant pour faire des maths... Pour une même fonction, je pourrais changer les notations en x = y(f) et dans ce cas, f serait l'entrée, x la sortie et y le nom de la fonction. Pour autant ce serait exactement la même relation entre l'entrée et la sortie qui serait représentée. Ce ne sont pas les étiquettes que tu colles sur l'entrée, la sortie ou la fonction qui font la fonction. De la même façon que ce n'est pas l'étiquette que les autres te collent qui définit qui tu es.
Ceci étant bien clair, je t'énonce tout de suite les 10 points essentiels sur les fonctions, et pour te simplifier la vie, j'utilise la notation classique y = f(x) 😉 !
1
Toutes les fonctions peuvent se dessiner ou comme on dit dans notre jargon « se représenter graphiquement ». Pour cela, on place les entrées sur l'axe horizontal (appelé axes des abscisses) et les sorties sur l'axe vertical (appelé axe des ordonnées) et pour chaque valeur d'entrée on peut lire la valeur de sortie sur la courbe !
Illustration :
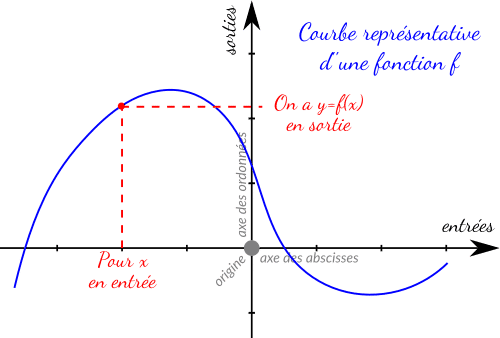
Remarque :
Il faut absolument t'aider de ça quand tu le peux. Peut-être que tu ne comprends rien aux maths quand il sont écrits, mais que tu comprends les dessins. Avec les fonctions, tu peux fortement t'aider des dessins pour comprendre les maths. Aussi, très souvent, tu pourras te faire une idée de la réponse juste en dessinant, il te suffira alors de la retrouver mathématiquement et c'est toujours plus simple que de faire un exercice à l'aveugle !
2
Pour une valeur x en entrée, il n’existe toujours qu’une seule valeur y en sortie. On dit que y est l’image de x par la fonction f.
Illustration :
En vert, la courbe représentative d'une fonction : on voit bien que pour chaque entrée il n'existe qu'une seule sortie. En rouge, un exemple de courbe qui ne représente pas une fonction puisque une entrée a 3 images !

Remarque :
Note ça bien dans ta tête, une valeur d'entrée n'a toujours qu'une seule image ! Si ce n'est pas le cas, ce n'est pas une fonction. Par conséquent, quand on te demandera de dessiner la représentation d'une fonction, pense bien au fait que tu ne peux pas avoir plusieurs images comme dans l'illustration de droite.
3
Pour une valeur y en sortie, il peut exister une ou plusieurs valeurs x en entrée qui ont y pour image. On dit que chacune de ces valeurs est un antécédent de y par la fonction f.
Illustration :

4
L'ensemble des valeurs x en entrée pour lesquelles f(x) a un sens s'appelle le domaine de définition de la fonction f. Par conséquent, pour n'importe quelle valeur x prise dans le domaine de définition; on peut calculer son image y par la fonction f.
Remarque :
C'est super important ! Une fonction est toujours définie sur un certain domaine, soit il est donné dans l'énoncé, soit c'est à toi de le trouver. Dans le dernier cas, il faudra simplement que tu cherches pour quelles valeurs d'entrée la formule n'est pas valide. Je te donne 2 exemples tout de suite.
Exemple :
Si tu repenses au fait que les fonctions représentent des relations entre deux quantités, il semble assez naturel qu'il y ait des moments pour lesquels ces relations n'aient pas de sens. Par exemple, si tu regardes la température (= sortie) qu'il fait dehors en fonction de l'heure (= entrée) qu'il est dans la journée, tu vois bien que celle-ci n'est pas définie pour les valeurs d'entrée négatives ! Le domaine de définition d'une telle fonction serait donc \mathbb{R}^+. Ou si tu prends la fonction f(x) = 1/x tu vois que pour x = 0, on ne peut pas calculer f(x). Son domaine de définition est donc \mathbb{R}^*.
5
Certaines valeurs de sortie n'ont pas d'antécédent. Autrement dit, étant donnée une valeur de sortie y, il n'existe pas toujours de valeur d'entrée x pour laquelle y=f(x).
Remarque :
Ce n'est pas grave ! Je veux juste que tu aies bien en tête que quand on te demande de trouver un antécédent, il est possible qu'il n'y en ait pas. Regarde l'exemple ci-dessous, ça devrait t'aider à t'en rappeler si c'est pas clair.
Exemple :
Je reprends l'exemple simple mais chiant du prix des fruits : le prix sera toujours positif (malheureusement !). Autrement dit, pour toutes les valeurs de sortie négatives (= prix négatif) il n'existe pas d'antécédent (= poids) par la fonction qui donne le prix en fonction du poids.
6
Une fonction f est croissante sur un intervalle I si pour des valeurs en entrée dans I qui augmentent, les valeurs en sortie augmentent aussi. Graphiquement, cela veut dire que la courbe représentative de f monte quand on la trace de gauche à droite. Mathématiquement, cela se traduit par le fait que si a < b avec a et b dans I alors f(a) < f(b).
Illustration :

7
Une fonction f est décroissante sur un intervalle I si pour des valeurs en entrée dans I qui augmentent, les valeurs en sortie diminuent. Graphiquement, cela veut dire que la courbe représentative de f descend quand on la trace de gauche à droite. Mathématiquement, cela se traduit par le fait que si a < b avec a et b dans I alors f(a) > f(b).
Illustration :

8
Le minimum (maximum) d’une fonction f sur un intervalle donné I est la plus petite (grande) valeur de sortie y=f(x) quand x appartient à I. Par conséquent, quelle que soit la valeur x dans I, son image y est plus grande (petite) que ce minimum (maximum).
Illustration :
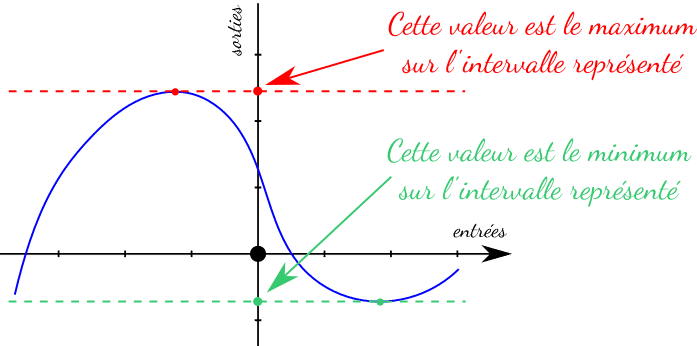
Remarque :
Si l'intervalle n'est pas précisé, c'est qu'on te parle du minimum ou du maximum sur le domaine de définition. Attention, il se peut qu'ils n'existent pas ! Par exemple, pour une fonction affine, il n'y a pas de minimum ou de maximum sur le domaine de définition. Par contre si on te demande le minimum sur un intervalle donné, il sera sur une des deux bornes de l'intervalle suivant si la fonction est croissante ou non (dessine-la et tu vas le voir !).
9
On dit qu’une fonction f est négative (positive) sur un intervalle donné I si les valeurs de sortie y sont négatives (positives) quelle que soit la valeur d’entrée x prise dans I.
Illustration :

Remarque :
Cette définition te parait un peu bête sûrement, et tu as raison, c'est du bon sens. Toutefois, elle va t'être utile quand tu vas commencer à utiliser les dérivées. La dérivée f' d'une fonction f étant elle-même une fonction, cette définition va te permettre de relier le signe (positif ou négatif) de f' avec les variations de f... c'est le point 10.
10
Une fonction f est croissante sur un intervalle I si sa dérivée f' est positive sur I. A l'opposée, f est décroissante sur I si f' est négative sur I.
Remarque :
Si tu n'as pas encore vu les dérivées, passe ce point ! Sinon, comme je te l'ai dit dans la remarque du point 9, on relie ici les variations d'une fonction avec le signe de sa dérivée. Si la dérivée est ‹‹ positive sur un intervalle ›› (définition du point 9) alors la fonction de départ est croissante (définition du point 6).
On y est, tu sais tout ce qu'il y a à savoir sur les fonctions pour pouvoir travailler sereinement avec. Aucun doute, si tu as bien compris ces 10 points et que tu les gardes en tête quand tu entends le mot ‹‹ fonction ››, tout va te sembler plus logique et plus simple. Pour finir, je te propose de tester de suite ce que tu as compris avec un QCM rapide !
Ça te semble plus clair ? Vérifie !
Explications
Autant dire que si tu comprenais rien aux fonctions en arrivant sur cet article, tu dois être en train de transpirer sévère ! Mais j'espère que ça te semble un peu plus clair. Prends quelques secondes pour respirer et assimiler ce que tu viens de lire, ça va t'aider. Aussi, pense à télécharger la Fiche Récap. si tu ne l'as pas encore, tout y est plus condensé et tu pourras la relire très rapidement et régulièrement pour que ça rentre !
Voici donc un petit QCM rapide qui va te permettre de tester si tu as bien saisi les 10 points essentiels que je t'ai listés. Dans un futur article, je t'expliquerai les astuces pour bien réussir un QCM et être le plus sûr possible de tes réponses. Mais pour le moment fais comme tu as l'habitude, pense juste à prendre ton temps. A toi de jouer, toutes les réponses sont données dans la Fiche Récap. avec des explications détaillées !
Teste ta compréhension avec ce QCM !
ATTENTION : Plusieurs réponses peuvent être possibles.
Question | A | B | C |
|---|---|---|---|
1. Une fonction affine peut être croissante sur un intervalle et décroissante sur un autre intervalle | Vrai | Faux | Ni l'un, ni l'autre |
2. La fonction affine f(x) = 2x + 2 est positive sur... | [5, 20] | [-10, 0] | [-1, 100] |
3. Quelles courbes représentent des fonctions ? 
| 1 et 3 | 2 | 2 et 3 |
4. D'après le graphique, un antécédent de 2 est... 
| 2 | 0 | -3 |
5. L'image de 2 par la fonction f(x) = 2x^2 - 8 + x est | 0 | 2 | -2 |
6. Si f(2) < f(5), on peut dire que f est... | Croissante | Décroissante | On ne peut pas dire |
7. Soit a et b deux réels dans l'intervalle [5, 10]. On sait que si a < b alors f(b) < f(a). On peut dire que f est... | Croissante sur [5, 10] | Décroissante sur [5, 10] | On ne peut pas dire |
8. Le domaine de définition de f(x) = \sqrt{x+2} est... | [2, +\infty[ | ]-\infty, -2] | [-2, +\infty[ |
9. D'après le graphique, le maximum de la fonction f est... 
| 17 | -3 | 6 |
10. Sachant que la dérivée de f(x) = 1/x est f'(x) = -1/x^2, on peut en déduire que la fonction f est... | Décroissante sur \mathbb{R}^* | Croissante sur \mathbb{R}^* | Décroissante sur ]0, +\infty[ |
Alors comment tu as trouvé ce QCM ? Vas vite voir les réponses et surtout les explications que je t'ai mises dans la Fiche Récap. pour savoir si tu avais bien tout compris ! En plus de ça, tu y trouveras d'autres exercices avec leurs réponses détaillées. Normalement avec tout ça, ta vision des fonctions devraient fortement s'améliorer !
Dis-moi dans les commentaires si cet article t'a permis de prendre du recul sur les fonctions et pose-moi les questions qui restent encore sans réponse pour toi !
Au plaisir de t'aider à réussir,
Steven



Je suis vraiment ravi d’avoir connue cette page. Ceci m’a beaucoup aidé à comprendre ce que je considère comme abstrait.
Merci beaucoup à vous
Top !
Bravo!! Très très bien expliqué et illustré !!
Bravo !!! Explications vraiment claires !!