Optimisation : l’Efficacité grâce aux Maths !

Seules les Maths permettent d'obtenir la solution Optimale !

Tu as lu l’article sur les fonctions ? Ou plus généralement, tu demandes à quoi peuvent servir les fonctions dans la « vraie vie » ? Eh bien, cet article est là pour te donner une première réponse concrète ! Ça me semblait intéressant de te donner rapidement des exemples d’utilisation de cet outil mathématique que sont les fonctions, et on commence avec l'Optimisation

C'est pourquoi j'ai décidé de te parler du domaine de l’Optimisation qui, comme son nom l’indique, consiste à utiliser les Maths pour « optimiser » ! Autrement dit, à trouver LA meilleure solution. Génial non 😉 ? Dis comme ça, ça semble utile ! Mais tu te demandes sûrement : la meilleure solution à quoi, optimiser quoi ? En fait, on peut optimiser beaucoup de choses sous des tonnes de formes, mais je vais surtout m'attarder sur tout ce qui se décrit avec des fonctions...

Je t’en dis beaucoup plus dans l’article, mais par exemple on optimise la forme des ailes des avions pour économiser du carburant. Ou la combustion du moteur de ta future voiture suivant la pression d’injection de l'essence. Mais aussi le trajet du livreur de colis pour lui faire gagner du temps. Ou pour finir la distribution des données sur le net pour maximiser le débit. Et tout ça grâce aux Maths !

l'Optimisation, un domaine des Maths à part entière.

La Meilleure solution grâce à l'Optimisation.

L’optimisation est un vieux domaine des mathématiques pour une bonne raison : à quoi servent les maths si on ne peut pas s’en servir pour résoudre des problèmes de la vraie vie ? Et encore mieux, pour trouver La Meilleure Solution ! En fait, le verbe Optimiser vient du latin Optimum qui signifie Meilleur. D'où la définition de l’optimisation : utiliser les maths pour trouver la solution optimale à un problème.

Très souvent, il est impossible de tester toutes les solutions possibles dans la vraie vie pour des raisons de temps ou de budget et de voir celle qui fonctionne le mieux. Donc plutôt que d’essayer, on écrit le problème sous forme mathématique et on cherche la meilleure solution par les Maths. En général, c'est bien plus rapide et beaucoup moins cher ! Une fois qu’on l’a trouvée, il ne reste qu'à la mettre en œuvre dans la vraie vie (et à vérifier que ça marche bien 😉 ).

Si tu as lu l’article que j’ai écrit sur les fonctions, il y a un lien évident entre fonction et optimisation. Est-ce que tu le vois ? D'un côté, les fonctions servent à décrire comment une quantité dépend d'une autre. De l'autre,  l'optimisation cherche à trouver la meilleure solution (pour une quantité donnée) en faisant varier un paramètre (l'autre quantité). Donc l'optimisation va se servir à fond de la fonction qui décrit la relation entre la solution qu'on cherche et la quantité dont elle dépend.

La Réalité est plus complexe...

Évidemment dans la vraie vie, les problèmes sont plus complexes et dépendent de beaucoup de paramètres. Mais l’idée reste exactement la même ! Peut-être que tu t'en doutes, mais la notion de fonction peut se généraliser pour décrire une quantité en fonction de plusieurs paramètres… et c’est ce qu’on fait. En voici un exemple simple.

Quand tu fais vibrer une corde de guitare, le son (c.à.d. la fréquence de vibration) que produit cette corde dépend de la tension de la corde, de son diamètre, de la force avec laquelle tu l’as mise en vibration. Et on pourrais même ajouter de la température de la pièce par exemple. Au final, il existe une fonction qui donne la fréquence de vibration en fonction de tout le reste !

Les 3 étapes d'une optimisation réussie.

1. La Modélisation

Premièrement, on modélise le problème. Autrement dit, on traduit le problème de la vraie vie en langage mathématique. Comme je te l'ai dit plus haut, le problème peut être traduit sous forme de fonctions. Mais on peut aussi le traduire en équations plus ou moins complexes, en probabilités ou encore en « stratégies ».

Comment fait-on ça de nos jours ? C’est un métier ! Il y a des gens pour qui le travail est de créer des modèles (sous forme mathématique) qui représentent le problème qu’ils essaient de résoudre. Pas besoin d’aller chercher bien loin pour trouver des exemples puisque ça fait des siècles que des gens cherchent à modéliser la nature !

En voilà donc un : on t’a dit en cours de physique que le poids c'est la masse multipliée par « petit g ». Tu t'en rappelles, ce ‹‹ petit g ›› s'appelle l’accélération de la pesanteur. Eh bien, c’est un très bon modèle pour représenter la force qu’exerce la Terre sur nous en fonction de notre masse ! Mais si on s'éloigne de la surface, ce modèle n'est plus assez précis et il en existe un autre.

2. L'Optimisation

Ensuite vient le moment de l'optimisation. C'est à dire le moment de chercher la (ou une) solution optimale au problème qu’on a modélisé durant la première étape. Ça peut prendre des tonnes de formes différentes, mais pour te donner un exemple compréhensible, je vais te parler d’aile d’avion.

En physique, on sait qu'il existe une relation très forte entre le profil d’une aile d’avion et deux caractéristiques importantes. D'une part sa portance qui est la capacité à « s’appuyer » sur l’air et donc à faire voler l’avion. D'autre part sa trainée qui est la « résistance au vent » et qu'on peut lié très directement à la consommation de carburant. Pour faire simple, plus ça résiste plus on consomme.

En conséquence, ce qu’on cherche à faire, c’est optimiser le profil de l’aile pour maximiser la portance tout en minimisant la trainée. Tout ça sans oublier une contrainte importante : le profil obtenu doit être réaliste et pas juste une solution mathématique. Autrement dit l’aile qui en découle doit avoir les bonnes caractéristiques pour finir sur un vrai avion. Typiquement, elle doit être très résistante aux turbulences ou encore avoir un coût de fabrication raisonnable.

Si ce sujet t'intéresse, regarde ce site et cet autre site qui résultent de TPE de 1ère. Ils sont bien faits et très accessibles.

3. Le Retour à la Réalité

Enfin, c'est le moment de grâce, celui du retour à la réalité ! Non seulement, il faut mettre en œuvre la solution qu’on a trouvée à l’étape précédente, mais il faut aussi s'assurer qu'elle donne les bons résultats. Normalement, si toutes les contraintes de la vraie vie ont bien été considérées en amont, la solution doit être fonctionnelle.

Sinon... euh c’est embêtant voire dangereux. Par exemple, une aile d’avion qui va casser à la première secousse. Dans ce cas, c'est qu'il y a eu un problème dans une des deux étapes précédentes. Soit le modèle de départ est faux ou pas assez précis. Soit on a raté l'optimisation et on doit se remettre aux maths sérieusement !

Évidemment, il y a tellement de paramètres à prendre en compte dans la vraie vie, qu'il est difficile de tout maîtriser. En général, on simplifie le problème en ne s'intéressant qu'aux paramètres qui influent le plus sur notre solution. Ensuite on utilise des méthodes mathématiques qui sont connues pour donner de bons résultats. Et enfin on contraint suffisamment l'optimisation dès le départ pour que la solution finale ait les bonnes caractéristiques !

J'espère qu'au travers de ces quelques exemples réels, j'ai réussi à te montrer qu'on utilise vraiment les maths pour trouver des solutions à des vrais problèmes. Pour finir cet article, je te propose de suivre exactement ces 3 étapes sur un problème à ton niveau, simple mais vraiment lié à la réalité. On va optimiser l'angle avec lequel tu dois lancer un truc pour qu'il aille le plus loin possible...

Optimisons à ton niveau !

Dans la partie que tu viens de lire j’ai essayé de rester le plus clair possible tout en évitant d’aller trop dans les détails car ça peut vite devenir très complexe ! Maintenant je vais faire l’inverse sur un exemple simple. Autrement dit, je vais détailler les 3 étapes de l’optimisation d’un problème qui utilise des notions de lycée.

Le but est de trouver l’angle optimal avec lequel lancer un truc (javelot, poids, manette, portable...) pour qu’il aille le plus loin possible. Cet exercice est là pour te montrer ce que peut donner l’optimisation du début à la fin sur un vrai problème.

1. L'équation de la trajectoire...

Le cadre

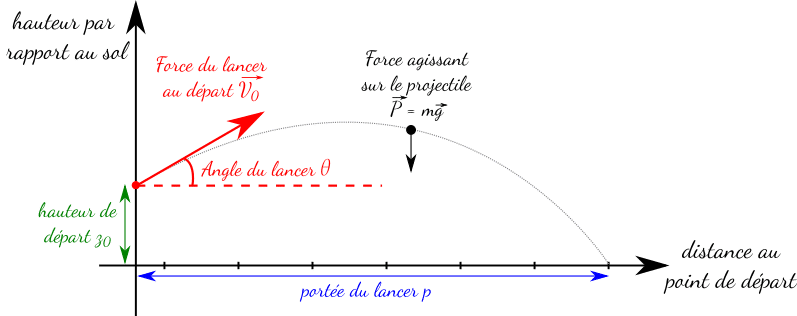
Tout d'abord, puisqu'on veut savoir à quelle distance le truc atterri, il faut trouver la trajectoire qu'il va suivre. On va prendre un cadre un peu simplifié, mais qui reste pertinent. On considère que tout se passe en 2D puisque si tu lances pas trop mal, le truc va partir tout droit, et que le sol est plat. De plus, on va négliger les forces de frottement de l’air. Ce qui fait qu'une fois lancé, seul le poids va agir, via l'accélération de pesanteur g, pour le faire retomber au sol.

Les hypothèses

Fixons la hauteur de départ du truc à une valeur z_0 car tu ne peux pas vraiment jouer dessus vu que c'est ta taille ! Il ne reste alors que deux paramètres qui influent sur la trajectoire : la force et l'angle avec lequel le truc est lancé. Il semble clair que plus tu vas mettre de force, plus il partira vite et ira loin. Par conséquent, on oublie le paramètre force en fixant la vitesse du truc au départ à une valeur V_0. Ainsi, il ne reste que l'angle qui joue sur la trajectoire. Enfin vu ce qui nous intéresse, une seule quantité en sortie est important : la distance qu’il parcourt avant de toucher le sol, aussi appelée portée.

La fonction ‹‹ portée en fonction de l'angle ››

Bon on y est, on sait ce qu'on veut voir en sortie, la portée p, et en fonction de quel paramètre en entrée, l'angle \theta, il ne reste plus qu'à trouver la formule de la fonction p(\theta) qui relie les deux ! J'épargne tes yeux mais tu peux quand même être curieux et regarder tout le cheminement pour trouver la formule en cliquant sous la formule ! Voici donc cette fameuse fonction :

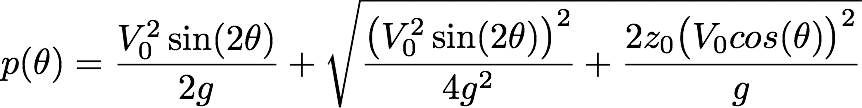
Où je te rappelle que g, V_0 et z_0 sont connus, la formule ne dépend donc bien que \theta.

2. L'angle Optimal pour lancer loin !

Étude graphique de la fonction

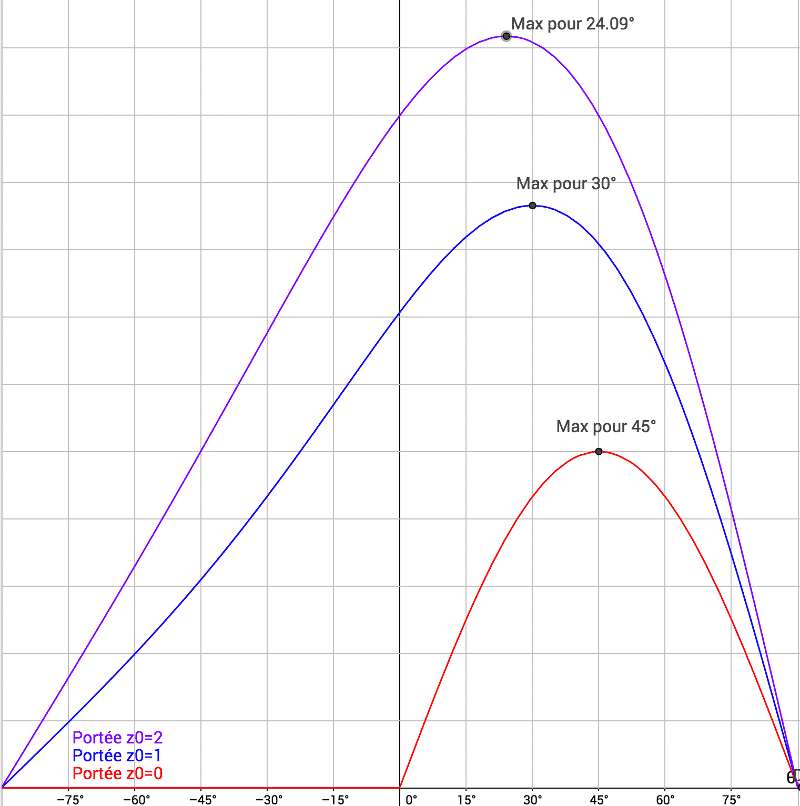
Puisque la fonction reliant l'angle et la distance est maintenant connue, on va l'utiliser pour trouver quel est l’angle optimal pour atteindre la portée maximale. Mais avant toute chose, réfléchissons un peu ! On a dit que z_0 est fixe car c'est en gros ta taille. Pour autant, ça ne veut pas dire qu'il ne joue pas sur la portée. Jetons un œil aux courbes représentatives de cette fonction p pour 3 valeurs de z_0, 0, 1 et 2 mètres de haut.

Ces courbes représentent la portée en fonction de l'angle (qui varie de -90° à gauche à +90° à droite) donc plus la valeur est haute plus le truc va loin. Quand on regarde ces courbes une chose saute aux yeux, l'angle pour lequel on atteint la portée maximale dépend de la hauteur z_0 de départ. Comme je le disais plus haut, ce n'est pas très étonnant. En effet, si tu lances de 100m de haut, tu iras plus loin que si tu lances du ras du sol !

Si jamais tu trouves la courbe rouge bizarre, n'oublie pas qu'elle représente un lancer d'une hauteur nulle. Donc tu ne peux pas lancer ‹‹ sous toi ››, autrement dit avec un angle négatif. Si tu ne le vois pas, jette un œil à l'illustration de la situation au dessus, un angle négatif veut dire que la flèche V_0 pointe vers le bas et non vers le haut comme dessiné.

On en déduit quoi de tout ça ?

On a maintenant tout ce qu'il faut pour trouver l'angle avec lequel tu dois lancer le truc pour qu'il aille le plus loin possible. Il suffit de fixer la vitesse initiale du lancer, ta taille comme hauteur initiale et tu vas pouvoir trouver l'angle optimal ! Comme on est tous différents, je t'ai fait un graphique interactif GeoGebra.

De la même façon que pour l'influence de la hauteur initiale, il est clair que la vitesse avec laquelle tu le lances va changer la courbe.  Par conséquent, l'angle optimal va aussi changer (sauf si z_0=0...) ! Dans GeoGebra tu peux observer tout ça, pense juste que la vitesse initiale est exprimée en m/s et que 6 m/s c'est environ 21.6 km/h.

Aussi, pour te simplifier la vie, je t'ai mis le calcul du maximum de la fonction. Donc dans la colonne de gauche tu as un couple de réel pour la valeur de A qui correspond à (\theta_{optimal}, p_{max}) où p_{max} est la portée maximale que tu vas atteindre en mètre.

Au fait, comment on trouve le maximum avec les maths ?

Au final, tu vois en jouant avec GeoGebra qu'on peut trouver l'angle optimal qui va te permettre de lancer le plus loin possible. Mais tout ça c'est graphique ! Alors comment on retrouve ces valeurs avec les Maths ? Pour faire ‹‹ simple ››, il suffit de chercher les variations de la fonction p. Puisque l'angle pour lequel elle passe de croissante à décroissante est l'angle optimal. Et pour trouver les variations, il faut dériver la fonction p par rapport à theta et regarde son signe. Ainsi, l'angle pour lequel la dérivée s'annule en passant de positive à négative est l'angle optimal ! Je te passe les calculs mais si ça t'intéresse, je te développerai tout ça avec plaisir. Même si je te préviens, les formules sont très très moches...

3. Et maintenant, on fait quoi ?

Le retour au monde réel : la prochaine fois que tu feras du lancer de truc dans le but d’aller le plus loin possible, pense à faire de l'optimisation pour calculer quel est l'angle optimal qui correspond à ta taille 😉 ! Et dis-moi si ça a fonctionné.

Voilà j'espère qu'à travers cet article sur l'optimisation mathématique, j'ai pu t'apporter un exemple plutôt  clair et concret de l'utilité des fonctions !

Dis-moi dans les commentaires si tu aimes savoir à quoi servent les maths et si t'as envie que je te détaille d'autres applications ?