Extraire tous les points avec la méthode JUS

Pas besoin d'en savoir plus pour améliorer tes notes en Maths.

Tu en sais déjà bien assez pour avoir une meilleure moyenne que celle que tu as actuellement ! Dis-moi, es-tu sûr d'extraire tous les points que tu es capable d'extraire de chaque exercice pendant les contrôles ?

Tu n'es pas évalué sur ce que tu sais...

...mais sur ta capacité à montrer ce que tu sais dans des conditions bien particulières : le ‹‹ contrôle ››. Et c'est hyper différent que d'être noté sur ce que tu sais vraiment. En fait, on peut trouver mille raisons d'expliquer que tu n'arrives pas à montrer à 100% ce que tu sais en contrôle. Par exemple, le stress conscient ou inconscient, l'énoncé tordu d'un exercice, le peu de sommeil de ta nuit précédente, etc.

Par conséquent, en savoir plus en maths c'est bien, mais ça ne fera pas tout. Car tu auras beau savoir plein de trucs, si tu ne sais pas le montrer le jour du contrôle, tu auras toujours des notes moyennes. A l'opposé, si tu apprends à ‹‹ montrer tes capacités ›› tu seras capable d'augmenter ta moyenne sans avoir besoin d'en savoir plus. Autant jouer sur tous les leviers !

Dans cet article, je te donne une méthode simple, la méthode JUS, pour extraire tous les points que tu es capable d'avoir avec ce que tu sais déjà !

Il n'y a rien à savoir pour avoir la moyenne !

Les 10 points faciles d'un contrôle

J'exagère un peu la formule mais ce n'est pas complètement faux ! En réalité, j'aurais dû dire : Il n'y a rien à savoir de ce que tu as appris cette année pour avoir la moyenne ! Autrement dit, si tu maitrises raisonnablement les maths des années précédentes, tu as ce qu'il faut pour avoir la moyenne. Pourquoi ?

Parce qu'un contrôle est fait de telle sorte que le plus grand nombre d’élèves ait la moyenne. Et pour atteindre ce résultat, il n'y a pas 50 manières : il y a toujours 10 points faciles à prendre… Encore faut-il savoir les ‹‹ chasser ››* ! Car comme je le postais il y a peu sur mon facebook ‹‹ dans les Maths, tout est simple mais le plus simple est difficile ››.

*Note que cette remarque sur les 10 points faciles à prendre est aussi vraie dans toutes les matières scientifiques.

Où je veux en venir ? Au fait que si tu connais les bonnes méthodes pour extraire tous les points faciles d'un contrôle, tu vas rapidement assurer la moyenne et il te restera du temps pour viser une bonne note !

Ok, mais ils sont où ces 10 points ?

Ok la théorie c'est génial : il y a 10 points faciles dans un contrôle. Mais tu n'as jamais la moyenne ou tu galères pour l'avoir ? Conclusion : T'es nul ? Non 😉 ! Je ne peux pas te demander de savoir faire un truc qu'on ne t'a jamais appris.

Non seulement on ne t'a surement jamais parlé des 10 points faciles, mais plus gênant à mon avis, on ne t'a pas appris à aborder un contrôle. Alors que comme je le disais au début, tu es noté sur ta capacité à ‹‹ restituer ce que tu sais en contrôle ››. Et pas seulement sur ce que tu sais. Et pour extraire tous les points faciles, ce n'est pas ce que tu sais en Maths qui va t'aider en priorité ! Voilà pourquoi je ne veux pas faire que des articles techniques sur les Maths, ça ne suffit pas pour être bon.

Cet article est donc le premier d'une liste qui t'expliquera comment assurer à 100% en contrôle ! Ici, je te détaille la méthode que j'ai mise au point pour extraire tous les points que tu es capable d'avoir avec ce que tu sais déjà. Je l'ai nommée la Méthode JUS comme ‹‹ Je lis tout - Une par une - Sans lâcher ›› !

La méthode ‹‹ JUS ›› pour extraire tous les points d'un exercice

Enfin, on y est, voici la méthode dont je te parle depuis le début pour que tu sois capable d'extraire tous les points d'un exercice qui contient plusieurs questions reliées ensemble. Elle se compose des 3 étapes que voici :

J comme ‹‹ Je lis tout ››

La première chose à faire quand tu commences un exercice, c’est de te dire ‹‹ Je lis tout l’exercice ››. C'est ultra important ! Il y a 2 raisons pour lesquelles tu dois absolument commencer par ça :

Et dans les faits ça donne quoi ? Tu lis la Question 1, tu essaies de comprendre le sens, tu lis la Question 2, tu essaies de comprendre le sens et de faire le lien avec la question précédente, tu lis la Question 3, tu essaies de comprendre le sens et de faire le lien avec les questions précédentes, ...

Attention, il faut aller assez vite : pas la peine de passer 5 minutes sur cette étape ! Le but est que tu aies une idée de ce qui t'attend. Et non pas que tu aies résolu l'exercice dans ta tête. D'autant plus que pour la lettre U tu vas repasser dessus.

U comme ‹‹ Une par une ››

La deuxième chose à faire est de relire les questions ‹‹ une par une ›› et d'identifier celles qui sont indépendantes. Autrement dit, d'identifier les questions qui n’utilisent pas les résultats des questions précédentes. Dans les faits, ce n'est pas toujours simple ! Donc essaie d'identifier les questions que tu penses indépendantes et fais une marque à côté. Quoi qu'il arrive, tu vas repasser dessus pour la lettre S, donc ce n'est pas grave si tu te trompes.

Au fait, à quoi ça sert de connaitre les questions indépendantes ? Premièrement, tu sauras qu'il y a des questions auxquelles tu pourras répondre même si tu es resté bloqué à la question d’avant ! Dans l'objectif d'aller extraire tous les points, ça semble une bonne idée. Deuxièmement, ça te fait faire une deuxième passe sur l'exercice entier et ça va affiner ta vision globale.

En général c'est assez évident, mais parfois pas... Par exemple, si on te demande de démontrer un résultat à la Question 1 et que la Question 2 n'utilise que ce résultat, la Question 2 est bien une question indépendante. En effet, même si tu n’as pas réussi à démontrer le résultat, tu peux et dois l’utiliser pour essayer de répondre à la Question 2 !

J'insiste...

Avant de passer à la dernière étape (qui n'est d'autre que faire l'exercice...), j'insiste sur le fait que ces 2 étapes J et U doivent être rapides. En contrôle, tu n'as pas le temps de les faire parfaitement, donc fais de ton mieux mais ne reste pas bloqué. En gros, tu lis la question et tu te poses aussitôt la question de l'étape. Ensuite tu essaies d'y répondre en quelques secondes et tu continues. Au final, ça doit te prendre à peine plus de temps que de lire l'exercice.

S comme ‹‹ Sans lâcher ››

Maintenant que tu as fait tout le travail de débroussaillage avec les étapes J et U, c'est le moment de faire l’exercice. Là pas de truc fou, tu te concentres à fond et tu réponds aux questions les unes après les autres ‹‹ sans lâcher ››. Qu'est ce que je veux dire par là ? N'abandonne pas à la première impression que tu n'y arriveras pas ! Laisse du temps à ton cerveau pour analyser et résoudre. Si la solution ne te vient pas de suite, elle pourrait bien te venir 2mn après.

Bien sûr, il y aura des moments où tu seras vraiment bloqué sur une question. Dans ces cas là, ne lâche pas l'exercice et passe à la question d'après ! C'est ça aussi ‹‹ sans lâcher ››. Car même si tu n'avais pas identifier la question comme indépendante, peut-être que tu vas t'apercevoir que c'en est une. De toute façon, ça ne coûte vraiment pas grand chose de faire cela... Si elle n'est pas indépendante, tu passes à la suivante, si elle l'est tu essaies de la résoudre ! De cette manière au moins tu seras sûr d’avoir pressé le citron jusqu’au bout 😉 !

Se concentrer c'est difficile, changer de sujet encore plus !

Non seulement ce n'est pas facile de se concentrer et de faire travailler son cerveau à 100% sur une tâche particulière. Mais c'est encore plus difficile de le faire changer de sujet de concentration. C'est la raison pour laquelle cette méthode est efficace pour tirer le meilleur d'un exercice. Dans les étapes J et U, tu t'imprègnes du sujet de l'exercice et tu forces ta concentration. Dans l'étape S, ton cerveau bosse à fond et surtout reste concentré sur le sujet de l'exercice actuel. De cette manière, tu maximises le temps que tu passes très concentré sur un sujet bien précis. Et donc les chances de trouver la solution. Autrement dit, d'extraire tous les points de l'exercice avec ce que tu sais et que ton cerveau peut utiliser.

On passe tout de suite à un exemple où je te détaille pas à pas comment cette méthode s'applique en conditions réelles.

L'exemple pas à pas.

C'est la fin de la théorie, on passe à la pratique. Pour cela, j'ai conçu un petit exercice avec 6 questions qui sont volontairement d'un niveau collège pour bien illustrer la méthode JUS. Voici son énoncé :

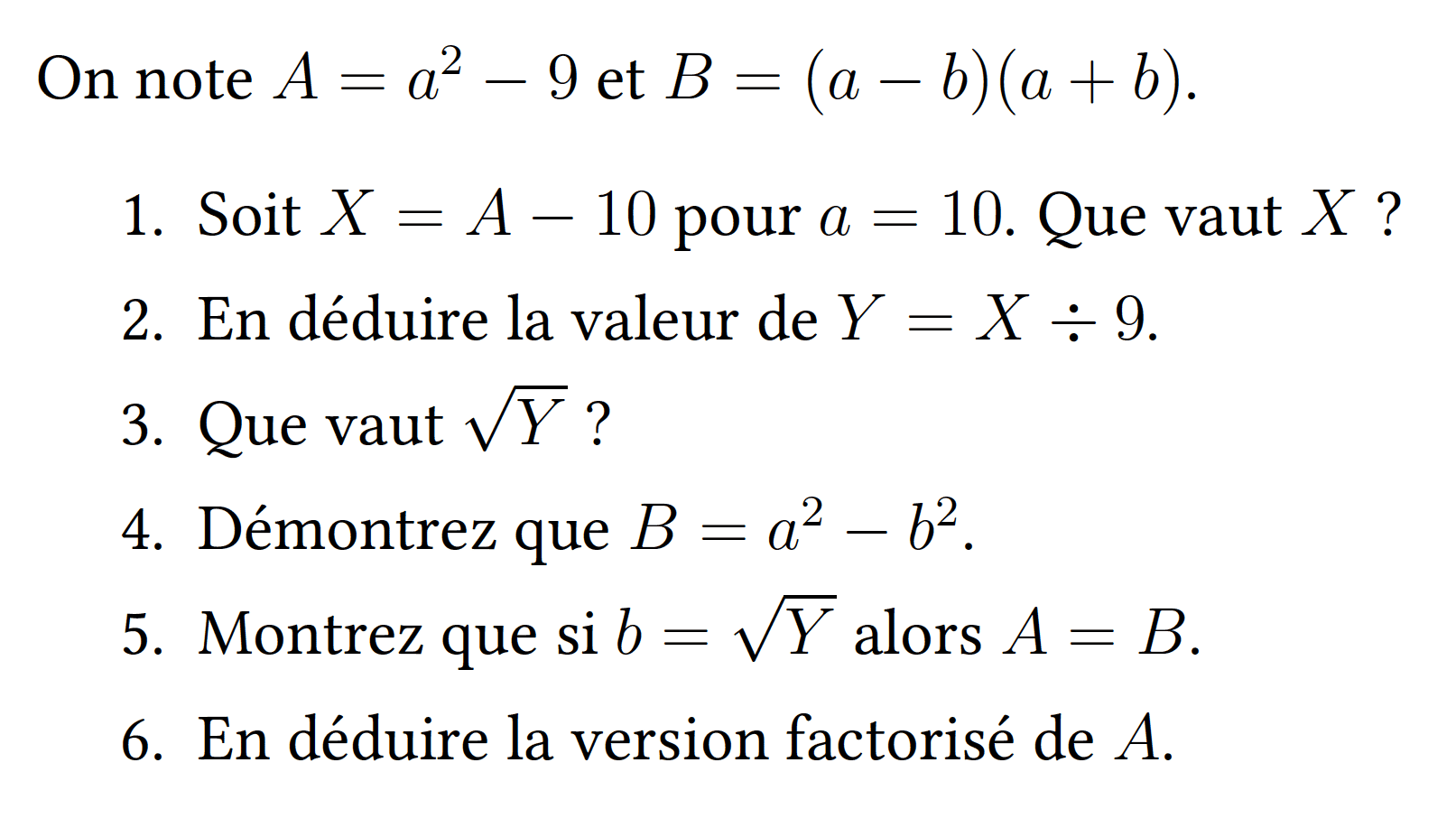
Je te détaille maintenant les étapes de la méthode JUS pour en extraire tous les points en faisant comme si je découvrais l'exercice en contrôle.

D'abord le J...

Premièrement ‹‹ Je lis tout ›› en commençant par l'énoncé ! La première ligne me dit que j'ai 2 formules qui définissent les valeurs de A et B en fonction de a et b. Je les note sur mon brouillon.

Dans la première question, on me demande de calculer une nouvelle valeur X qui s'écrit en fonction de A. Ca devrait le faire. On continue avec la question 2 où je dois déduire la valeur d'un nouveau Y en fonction du X calculé à la question 1. Si tout se passe bien en 1 ça devrait aussi être bon pour le calcul de Y. Question 3, on calcule la racine de Y, facile. Alors dans la question 4, on repasse sur B et je dois démontrer une formule, ça m'a l'air un peu obscur mais bon on verra. J'enchaîne avec la question 5, bon Y est de retour, on mélange le début de l'exercice avec la fin, à voir. Enfin la dernière question, on revient à A avec une question qui me parle de factorisation...

Voilà une première passe rapide, qui permet de voir qu'on fait quelques calculs dans les questions 1 à 3. Puis que la question 4 a l'air un peu à part. Et qu'enfin on retrouve les trucs des questions du début dans les deux dernières questions. C'est flou, mais c'est une première passe, donc c'est OK.

Ensuite le U...

Deuxièmement, je vais relire les questions ‹‹ une par une ›› et chercher à identifier les questions indépendantes. De façon plus général, on cherche en fait à identifier les dépendances entre les questions.

C'est parti avec la première question qui est nécessairement indépendante de la question d'avant qui... n'existe pas ! La question 2 demande d'utiliser un X qui n'apparait pas dans l'énoncé et qui apparait dans la question 1. Idem en question 3, qui fait apparaitre le Y de la question 2. Donc ces 2 là ne sont pas indépendantes des précédentes.

En revanche, seuls a, b et B interviennent dans la question 4, elle ne dépend donc pas des questions 1, 2 et 3. Bonne nouvelle car si on bloque sur les 3 premières on pourra toujours faire celle-là. Bon... ça ne dure pas, le Y est de retour en question 5, donc pas indépendante.

Enfin dernière question, seul A apparaît, mais on demande d'‹‹ en déduire ›› donc c'est pas clair. On verra donc dans la phase S ! On est donc bons avec les étapes J et U, et comme prévu, ça nous a pas pris beaucoup de temps.

Enfin le S...

A ce moment-là, on est prêt à être efficace à 100%, on est bien rentré dans l'exercice et il n'y a plus qu'à s'y coller ! C'est parti.

En conclusion, j'espère que cet exemple t'a bien montré comment appliquer la Méthode JUS pour extraire tous les points d'un exercice même quand tu restes bloqué sur une question. N'hésite pas à me dire ce que tu en penses dans les commentaires ou à me poser tes questions !

Pour finir, un dernier conseil : dès que tu arrives en contrôle, tu notes la signification des 3 lettres de la méthode JUS sur ton brouillon. Et à chaque début d'exercice tu n'oublies pas que tu veux extraire tous les points ! C'est à dire tout le JUS de l'exercice...

Cet article t'a aidé ?
Partage ton sentiment dans les commentaires !