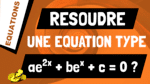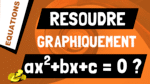Dans cette vidéo, on va voir comment déterminer le domaine de résolution dune équation qui contient des racines.
Qu’est-ce que le domaine de résolution ?
Donc on va chercher le domaine de résolution, autrement dit les x pour lesquels l’équation existe. On a donc une équation contenant des racines, que je vais écrire comme ça volontairement.
Alors là, encore qu’est-ce que c’est la contrainte ? Qu’est-ce qui va imposer une contrainte ? C’est le fait que racine de x est définie pour x strictement positif.
Autrement dit, ce qui est sous la racine doit être strictement positif. Ce qui fait que dans les faits ce que tu vas regarder si ce que ce qui est sous la racine est strict positif.
Comment déterminer le domaine de résolution d’une équation avec des racines : un exemple !
Alors on va prendre un truc un peu plus compliqué, (2x-1)/(x+2) par exemple. Et on va dire que c’est égal 2. Peu importe le chiffre ici ça nous intéresse pas, ce qui nous intéresse c’est les contraintes sur l’équation !
Première contrainte.
Donc cette équation est toute simple ici, alors il y a deux contraintes : celle qu’il ne faut jamais oublier, c’est la division par 0. La division par zéro nous dit quoi ici, elle nous dit que x + 2 doit être différent de 0, ça nous implique que x est différent de -2.
Ca c’est la première contrainte, c’est celle que tu as toujours sur les équations pour trouver le domaine résolution. Il faut pas que tu divises par 0 évidemment, puisque ça n’a plus aucun sens.
Deuxième contrainte.
La deuxième contrainte, c’est la racine ici. On a dit pour que la racine soit bien définie, il faut qu’elle soit positive, c’est-à-dire que ce qui est sous la racine soit positif.
Donc la deuxième contrainte c’est 2x-1 sur x+2 strict positif. Et c’est cette contrainte-là, en plus de celle là (puisqu’il faudra les cumuler) qui va te permettre de trouver le domaine de résolution de ton équation.
Petite étude de signe…
Alors ici 2x-1 / x+2 quand est-ce que c’est positif ? Eh bien, on étudie 2x-1, on fait un petit tableau de signe simplement, et on va avoir x, 2x-1, et x+2.
Puisque le signe d’une division comme le signe d’une multiplication est donné par la multiplication des signes. Alors on va avoir moins l’infini, plus l’infini et les valeurs remarquables.
Alors pour celles-ci, à quel moment on s’annule, on s’annule pour un 1/2 et pour la deuxième pour -2. Donc on a -2 et 1/2 ici. on vaut 0, ici on veut 0. Et donc ce qu’on va regarder ensuite, c’est le ratio 2x-1 / x+2.
Déjà on sait que c’est une valeur interdite -2, puisqu’on divise par 0 ça pose un problème. Maintenant comment on sait le signe avant après ?
Petit rappel sur les fonctions affines…
Ici, on est de la forme à ax+b c’est donc une fonction affine, et pour une fonction affine, la représentation graphique c’est une droite.
Le sens de variation est donné par le coefficient devant le x ici, c’est deux fonctions affines croissantes. Une fonction affine qui est croissante va couper à un certain point, par exemple, 1/2 ici, avant de couper puisqu’elle est croissante elle va être négative et ensuite elle sera positive.
Donc le domaine de résolution est…
Même chose ici. Donc là pour le ratio, quand le numérateur vaut 0, eh bien, on vaut 0. Quand le dénominateur vaut 0, c’est une valeur interdite. Et ensuite il reste le signe, positif*positif ça nous donne du positif.
Au milieu, on est sur négatif*positif donc ici on est négatif, et là on est négatif*négatif, ça fait positif. Qu’est ce qu’on en déduit ici ?
On en déduit que le domaine de résolution, enfin le domaine pour lequel ce ratio est positif c’est ]-∞,-2[, on ne prend pas-2, union 1/2…
Erratum…
Alors j’ai fait une petite erreur ici, la racine est bien définie pour x positif ou x nul. Donc ici on va bien prendre le 1/2… union [1/2, +∞[. D’accord donc le 2 le -2 il est déjà exclu, celui qu’on avait vu ici, donc il n’y a pas de problème, il n’a pas besoin. Donc ce domaine-là, c’est directement le domaine de résolution de l’équation.
Conclusion
Dès que tu as une équation, pour trouver son domaine résolution, tu enlèves tous les x qui font que certains termes ne sont pas définis.
Si tu divises par 0, tu enlèves la valeur de x pour laquelle la division se fait par 0. Après quand tu as une racine, eh bien, ce que tu fais c’est que tu t’assures que ce qui est sous la racine soit positif ou nul.
D’accord ici j’avais mis stricte, mais c’était une erreur, c’est bien positif ou nul ! Puisque √0 vaut 0.
Et donc quand tu as fait ça, et que tu as trouvé le signe (ça peut demander de faire un tableau signe comme je l’ai fait ici), eh bien, tu trouves le domaine de résolution de ton équation.
Donc voilà comment tu peux déterminer le domaine de résolution d’une équation contenant des racines.
Clique ici pour voir plus de vidéos sur ce thème, et abonne-toi à la chaine Youtube.