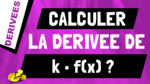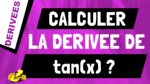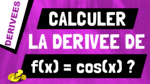Dans cette vidéo, je vais te montrer comment retrouver et calculer la dérivée de sinus x. Donc la dérivée de sin(x) c’est cos(x). Ok.
Comment est ce que tu te rappelles de la dérivée de sinus ?
Eh bien tu fais un cercle trigo ! Et il n’y a pas besoin qu’il soit beau comme tu peux voir. Ici tu as cosinus, ici tu as sinus, ça c’est important, tu le sais normalement. Puis ce que tu vas rajouter c’est -sinus ici, et puis -cosinus ici.
La chose importante à retenir c’est que quand on dérive, on tourne vers la droite. Donc dériver = 1/4 de tour vers la droite. Pour retenir ça, pas très compliqué, le « d » de droite et le « d » des dérivées, tu dérive à droite.
Maintenant quand on prend le sinus et qu’on veut le dériver, on fait 1/4 de tour à droite. Sur quoi on tombe ? Sur cosinus. Ça c’est top, ça nous dit que (sin(x))’ = cos(x).
Et donc là pas besoin de réfléchir, tu sais directement ta dérivée elle est ici, tu vas pas réfléchir au signe.
Et la dérivée de -sinus ?
De la même façon si tu as -sin(x), eh bien tu dérives en faisant 1/4 de tour à droite toujours. Donc tu vas tomber sur -cos(x). Donc ici (sin(x))’ = cos(x).
C’est la meilleure façon de ne jamais faire d’erreurs de signes dans les dérivées des fonctions trigo !
Clique ici pour voir plus de vidéos sur ce thème, et abonne-toi à la chaine Youtube.