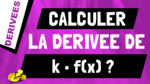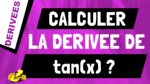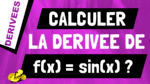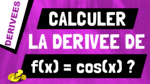Dans cette vidéo, on va voir ce que signifie qu’une fonction est dérivable en un point. Alors on va regarder si une fonction f est dérivable en un points a, qu’est ce que ça veut dire ?
Fonction dérivable en un point : l’idée « avec les mains ».
Vraiment avec les mains, très grossièrement ça veut dire que il n’y a qu’un seul nombre dérivé de f en a. Alors c’est vraiment avec les mains ici parce que c’est un peu tordu de le dire comme ça, mais ça veut dire quoi ?
Ça veut dire qu’en fait quand on regarde le nombre dérivé, si je le remets c’est la limite quand h tend vers zéro de f(a+h)-f(a) / h. Mais ici h, il tend vers zéro, il peut tendre par la droite c’est à dire par les valeurs positives de h ou par les valeurs négatives.
Si une fonction est dérivable, qu’on tende par les valeurs positives ou par les valeurs négatives, on va tomber sur le même nombre dérivé.
Alors c’est le cas dans la plupart des fonctions qu’on va voir en terminale. Mais de temps en temps c’est pas le cas !
Un exemple de fonction bien dérivable.
Par exemple ici, donc si je trace un repère et que je prends une fonction lisse comme ça. Et que je regarde un point a par exemple ce point ici, tu vois que tout est bien lisse. On a une tangente qui est bien définie qui est plutôt comme ça, voilà.
Vu que cette tangente elle est bien définie, elle est bien propre, tu vois que ton nombre dérivé ici, il va bien être défini. Puisque quant tu tends par ici ou par ici, tu as bien la même chose.
Un exemple de fonction non dérivable en un point.
Alors maintenant je vais donner un exemple de fonction pas dérivable. C’est la fonction valeur absolue de x ! Donc valeur absolue de x c’est une fonction qui a cette tête là, d’accord ?
Valeur absolue, si x est positif, on prend directement la valeur de x. Si x est négatif, on prend -x. Donc ici si on a x égal -1, valeur absolue de x c’est 1. x=-10, valeur absolue de x égale 10.
Tu vois qu’en zéro il risque d’y avoir un petit problème ! Parce qu’on a des droites un peu partout, ça pose pas de problème ça. Donc le taux de variation ici sur la partie à droite, il est défini directement par la pente de cette droite.
Pente à gauche et à droite en 0.
Donc ici puisqu’on a dit x c’est x, ici la pente c’est 1. Et de la même façon ici, la pente elle est négative mais elle est définie par la droite, donc pente = -1.
Vu que c’est des droites, les tangentes elles ont exactement la même pente, et la tangente à la droite eh bien c’est elle-même. Donc le taux de variation de ce côté là, il vaut 1, de ce côté là il vaut -1.
Autrement dit, tu vas pouvoir tendre, si on prend x=0 ici qui est la chose qui nous intéresse où a=0, tu vois que si on a la limite quand f(a+h) moins… Alors je vais le faire directement avec la bonne fonction, on a dit c’est la valeur absolue, (|a+h| – |a|)/h quand h tend vers 0 et h est positif, eh bien cette chose là ça vaut 1.
Maintenant si on le fait de l’autre côté, la limite quand h tend vers zéro mais h négatif de ((a + h) – a) / h, eh bien là c’est -1 puisque cette valeur là c’est toujours -1.
En fait le taux de variation de ce côté là, il est à -1, de ce côté là il est à 1. Quand on va tendre vers zéro, on a deux valeurs possibles : -1 ou 1. Ça ça veut dire quoi ? Eh bien ça veut dire que valeur absolue de x n’est pas dérivable en 0 simplement !
Voilà ce qu’est être dérivable en a. C’est simplement accepter un nombre dérivé en a. Et à partir du moment où il peut y avoir plusieurs nombres suivants par quel côté t’es arrivé, eh bien ce n’est plus dérivable.
Clique ici pour voir plus de vidéos sur ce thème, et abonne-toi à la chaine Youtube.