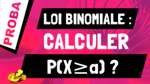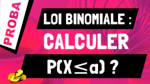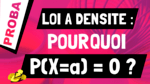Dans cette vidéo, on va voir comment calculer la probabilité p(a < X < b) quand X suit une loi continue.
Rappel sur les lois continues.
On sait que si X suit une loi continue, sa densité de probabilité f est une fonction positive dont l’intégrale sur R vaut 1. Eh bien, on veut calculer la probabilité que X, que la variable soit comprise entre a et b, combien ça vaut ?
Calculer p(a < X < b) quand X suit une loi continue ?
Même chose que dans la vidéo précédente, ici on va le dessiner parce que c’est important de le visualiser ! Donc on prend une fonction ici, et qu’est ce qu’on sait ?
On sait qu’elle est positive et que son intégrale vaut 1. Alors là, je vais en prendre une. Fais moi confiance, l’intégrale vaut 1 ici, et puis on a une cloche. C’est bien défini sur R, soit Df = R.
Regardons a et b.
Ce qui nous intéresse ici c’est d’avoir ‘a’ et ‘b’, alors on va prendre a plus petit que b sinon ça va être un peu moche. Par exemple, ici a et ici b. Et ce qu’on veut c’est connaître la probabilité que x soit entre ces deux valeurs. Sur l’axe des abscisses ici c’est les valeurs pour ta variable aléatoire X.
Calculer la proba.
Eh bien qu’est ce que ça va être ? Ça va être l’intégrale entre ces deux valeurs ! Et l’intégrale entre ces deux valeurs ici, puisque la fonction est positive, c’est bien l’aire sous la courbe ici que je suis entrain de hachurer.
Calculer p(a < X < b), c’est à dire la probabilité que X soit compris entre a et b, c’est calculer l’intégrale entre a et b de f(x) dx. Comment tu t’en rappelles ?
Comment s’en rappeler ?
Qu’est ce que c’est X compris entre a et b ici ? C’est X ∈ [a, b]. Alors ici que se soit ouvert et fermé, on s’en moque parce que sur les intégrales, on ne verra pas la différence ! (On verra ça dans une des vidéos suivantes).
Si tu retiens ça, que X compris entre a et b, ça veut dire que X appartient à [a, b], eh bien, la probabilité que X ∈ [a, b] c’est l’intégrale sur l’intervalle [a, b] de f(x) dx. Et l’intégrale sur l’intervalle [a, b] c’est la même chose qu’une intégrale entre a et b !
Calculer l’intégrale.
Maintenant, tu connais la fonction qui te sert de densité de probabilités. Donc tu connais une primitive de cette fonction. Et tu vas pouvoir donc calculer l’intégrale en calculant la primitive et en faisant F(b) – F(a). De cette façon-là, tu vas pouvoir calculer la probabilité de X compris entre a et b pour X suivant une loi continue.
Une alternative ?
Alors, une autre façon de faire qui est intéressante c’est de voir que cette aire ici c’est aussi l’aire comprise entre moins l’infini et b. Donc si je prolonge ici, on va dire ça c’est l’aire entre moins l’infini et b à laquelle on va soustraire l’aire entre moins l’infini et a.
Qu’est ce que ça nous donne aussi si on l’écrit différemment ? p(a < X < b) = p(X < b) – p(X < a). Ça c’est bien l’intégrale entre moins l’infini et b de f(x) dx, moins l’intégrale entre moins l’infini et a de f(x) dx.
Comprendre graphiquement…
Maintenant, si on combine les deux intégrales, évidemment on retourne entre a et b. Et ça c’est important de le comprendre graphiquement, c’est là que le graphique sert à quelque chose !
Tu vois que l’aire que j’avais mis en vert au départ ici, entre a et b, tu peux la calculer comme l’aire comprise entre moins l’infini et b, à laquelle tu vas soustraire l’aire entre moins l’infini et a.
C’est une autre façon de voir les choses. Tu vois graphiquement ici que c’est vrai et donc tu peux l’écrire aussi mathématiquement. C’est à dire que si l’aire entre moins l’infini et b c’est p(X<b), l’aire entre moins l’infini et a c’est p(X < a). Donc p(a < X < b) c’est aussi p(X < b) – p(X < a).
Typiquement, dans un exercice où tu as déjà calculé p(X < b) et p(X < a)… plutôt que d’aller refaire un calcul d’intégrale, tu vas directement utiliser cette formule là !
Et cette formule-là, elle est toute simple à visualiser. Voilà deux façons de calculer la probabilité p(a < X < b) pour une variable aléatoire X qui suit une loi continue.
Clique ici pour voir plus de vidéos sur ce thème, et abonne-toi à la chaine Youtube.